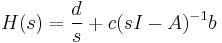Nonlinear control

Nonlinear control is the area of control engineering specifically involved with systems that are nonlinear, time-variant, or both. Many well-established analysis and design techniques exist for LTI systems (e.g., root-locus, Bode plot, Nyquist criterion, state-feedback, pole placement); however, one or both of the controller and the system under control in a general control system may not be an LTI system, and so these methods cannot necessarily be applied directly. Nonlinear control theory studies how to apply existing linear methods to these more general control systems. Additionally, it provides novel control methods that cannot be analyzed using LTI system theory. Even when LTI system theory can be used for the analysis and design of a controller, a nonlinear controller can have attractive characteristics (e.g., simpler implementation, increased speed, or decreased control energy); however, nonlinear control theory usually requires more rigorous mathematical analysis to justify its conclusions.

1 Properties of nonlinear systems
2 Analysis and control of nonlinear systems
3 Nonlinear feedback analysis – The Lur'e problem
- 3.1 Absolute stability problem
  - 3.1.1 Popov criterion
4 Theoretical results in nonlinear control
- 4.1 Frobenius Theorem
5 Further reading
6 See also

Properties of nonlinear systems

Some properties of nonlinear dynamic systems are

They do not follow the principle of superposition (linearity and homogeneity).
They may have multiple isolated equilibrium points.
They may exhibit properties such as limit-cycle, bifurcation, chaos.
Finite escape time: Solutions of nonlinear systems may not exist for all times.

Analysis and control of nonlinear systems

There are several well-developed techniques for analyzing nonlinear feedback systems:

Describing function method
Phase plane method
Lyapunov stability analysis
Singular perturbation method
Popov criterion (described in The Lur'e Problem below)
Center manifold theorem
Small-gain theorem
Passivity analysis

Control design techniques for nonlinear systems also exist. These can be subdivided into techniques which attempt to treat the system as a linear system in a limited range of operation and use (well-known) linear design techniques for each region:

Gain scheduling

Those that attempt to introduce auxiliary nonlinear feedback in such a way that the system can be treated as linear for purposes of control design:

Feedback linearization

And Lyapunov based methods:

Nonlinear feedback analysis – The Lur'e problem

An early nonlinear feedback system analysis problem was formulated by A. I. Lur'e. Control systems described by the Lur'e problem have a forward path that is linear and time-invariant, and a feedback path that contains a memory-less, possibly time-varying, static nonlinearity.

The linear part can be characterized by four matrices (A,B,C,D), while the nonlinear part is Φ(y) with $\frac{\Phi(y)}{y} \in [a,b],\quad a<b \quad \forall y$ (a sector nonlinearity).

Absolute stability problem

Consider:

(A,B) is controllable and (C,A) is observable
two real numbers a, b with a<b, defining a sector for function Φ

The problem is to derive conditions involving only the transfer matrix H(s) and {a,b} such that x=0 is a globally uniformly asymptotically stable equilibrium of the system. This is known as the Lur'e problem.

There are two main theorems concerning the problem:

The Circle criterion
The Popov criterion.

Popov criterion

The sub-class of Lur'e systems studied by Popov is described by:

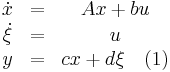
$\begin{matrix} \dot{x}&=&Ax%2Bbu \\ \dot{\xi}&=&u \\ y&=&cx%2Bd\xi \quad (1) \end{matrix}$

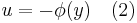
$\begin{matrix} u = -\phi (y) \quad (2) \end{matrix}$

where x ∈ Rⁿ, ξ,u,y are scalars and A,b,c,d have commensurate dimensions. The nonlinear element Φ: R → R is a time-invariant nonlinearity belonging to open sector (0, ∞). This means that

Φ(0) = 0, y Φ(y) > 0, ∀ y ≠ 0;

The transfer function from u to y is given by

$H(s) = \frac{d}{s} %2B c(sI-A)^{-1}b \quad \quad$

Theorem: Consider the system (1)-(2) and suppose

A is Hurwitz
(A,b) is controllable
(A,c) is observable
d>0 and
Φ ∈ (0,∞)

then the system is globally asymptotically stable if there exists a number r>0 such that
inf_{ω ∈ R} Re[(1+jωr)h(jω)] > 0 .

Things to be noted:

The Popov criterion is applicable only to autonomous systems
The system studied by Popov has a pole at the origin and there is no direct pass-through from input to output
The nonlinearity Φ must satisfy an open sector condition

Theoretical results in nonlinear control

Frobenius Theorem

The Frobenius theorem is a deep result in Differential Geometry. When applied to Nonlinear Control, it says the following: Given a system of the form

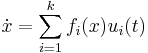
$\dot x = \sum_{i=1}^k f_i(x) u_i(t) \,$

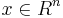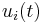where $x \in R^n$ , $f_1, \dots, f_k$ are vector fields belonging to a distribution $\Delta$ and $u_i(t)$ are control functions, the integral curves of $x$ are restricted to a manifold of dimension $m$ if span( $\Delta) = m$ and $\Delta$ is an involutive distribution.